Smith予測器によるむだ時間の補償
目次
はじめに
現実的なシステムは入力を与えてから出力に反映されるまでに遅れを有する場合があります.ごく一般的な線形システム,たとえばなども2次遅れ系などと呼ばれたりしますが,これらは実際には入力を与えて即座に応答が発生するようにモデル化されています.
一方で,入力を与えてからある時間だけ経過した後にようやく応答が発生するようなシステムを前者と区別して純時間遅れ系(Pure time delay system)と呼びます.
ただ今回はラフな形で「むだ時間(Dead time)」と呼ぶことにします.
むだ時間を持つシステムの具体例としては以下のようなものがあります.
- 熱伝達システム
- 長いヒモをもつクレーンの自動操縦
- 圧延
- ベルトコンベア上の製品に対する作業
- 長距離通信を介するシステム
このようなむだ時間を有するシステムの制御について考えてみます.
むだ時間を有するシステム
対象とするシステム
たとえば,圧延機は下図のような構造を持ちます.

上流から流れてくる金属板にローラで圧力を与え薄く引き伸ばす装置ですが,厚みを測定するセンサの位置が圧力を与える場所から一定の距離
離れているため,入力(圧力)を与えてから出力(厚み)が応答するまでに時間がかかります.
上記のようなシステムを伝達函数の形で表すと次のようになります.
\begin{align}
G(s)=\frac{\omega_{n}^{2}}{s^{2}+2\zeta\omega_{n}s + \omega_{n}^{2}}e^{-Ls}
\end{align}
ここでがむだ時間を表します.
また,これらのような空間的な広がりを持つシステムを分布定数系と呼ぶようです.
反対に,空間的な広がりのない一般的な線形システムなどは集中定数系と呼びます.
ステップ応答と安定性
具体的に,
としたときのステップ応答とナイキスト線図は以下のようになります.
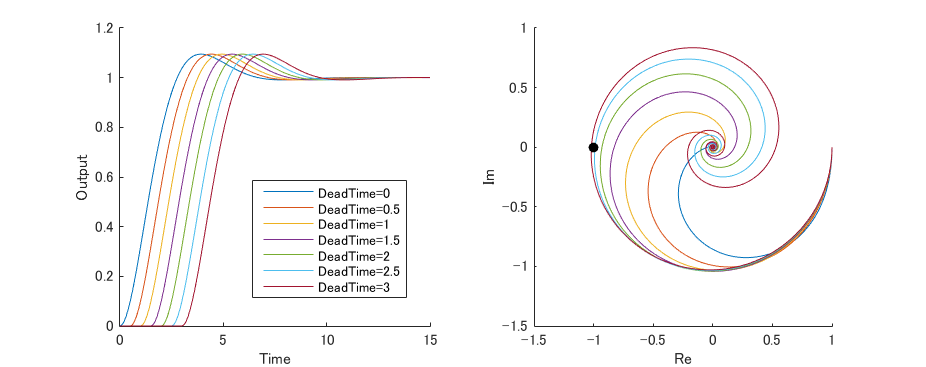
むだ時間が大きくなるとステップ応答波形は右方向へ,ナイキスト線図はの点から外側方向へ広がるように変化します.
ナイキスト線図において,開ループがの点
から軌跡が
の点を左手に見るように描かれていれば閉ループは安定,右手に見る場合があれば閉ループは不安定となります.
(開ループの特性を見ることで閉ループの安定性を議論しているところに注意が必要)
このため,このシステムは閉ループにした場合のとき安定,
のとき安定限界,
のとき不安定であることがわかります.
このときの閉ループとはゲインのP制御をすることに相当します.
このゲインを上げることで,軌跡は原点の点を中心として拡大され,これを基にして比例ゲインを決めることができるのですが,今回は割愛します.

今回は上記での場合について議論します.
この閉ループシステムは先に述べたように不安定なシステムとなります.
閉ループのステップ応答は下図のようになります.

青の実線はむだ時間がない場合,灰の実線がむだ時間がある場合です.
ナイキスト線図に戻ると,むだ時間がない場合には閉ループは安定になることがわかるかと思います.
むだ時間を有するシステムの閉ループ伝達関数は次のようになります.
\begin{align}
P(s)=\frac{K_{p}G(s)e^{-Ls}}{1+K_{p}G(s)e^{-Ls}}
\end{align}
ただし,はPゲインを表します.
このようにシステムがむだ時間を有する場合には,むだ時間の項が分母に現れるためフィードバックシステムの設計が困難になります.
Smith予測器
概要
このようなむだ時間を有するシステムを扱うための手法がSmith予測器(Smith predictor)です.
原著は以下のようですが,古いせいかwebからは探すことができませんでした.
なのでここではMathWorksのページを参考にしています.
O. Smith, "Closer control of loops with dead time", Chemical engineering progress, Vol. 53, No. 5, pp. 217-219, 1957.
Smith予測器を利用すると擬似的にむだ時間を閉ループシステムの外側に追い出すことができます.
Smith予測器では制御対象のノミナルモデル
が必要です.
簡単のためプラントとノミナルモデルのモデル化誤差がないものとします.
\begin{align}
G_{M}(s)=\frac{\omega_{n}^{2}}{s^{2}+2\zeta\omega_{n}s+\omega_{n}^{2}}
\end{align}
ここでノミナルモデルにはむだ時間を含まないことに注意が必要です.
具体的には下図のようなシステムを構成することになります.

プラントとノミナルモデルが等しい場合,この閉ループ伝達函数は以下の式と等価となります.
\begin{align}
P(s)=\frac{K_{p}G(s)}{1+K_{p}G(s)}e^{-Ls}
\end{align}
ここで,むだ時間のない場合におけるP制御の伝達函数は以下です.
\begin{align}
P(s)=\frac{K_{p}G(s)}{1+K_{p}G(s)}
\end{align}
両者を比較してみると,むだ時間がフィードバックループの外に出ていることがわかるかと思います.
改めてブロック図を書くと以下の図が得られます.

Smith予測器を利用することによって,むだ時間を閉ループの外側に追い出すことができました.
安定性の確認
このときの開ループにおけるナイキスト線図が下図となります.

青の実線がむだ時間なし,灰の実線がむだ時間あり,赤の実線がむだ時間ありのシステムにSmith予測器を適用した場合です.
Smith予測器を適用した場合には,軌跡がの点を左手に見ていることからシステムが安定となっていることがわかります.
ステップ応答の確認
実際の応答を確認してみます.

赤の実線がSmith予測器を利用した場合の応答,灰の破線がむだ時間のないシステムにフィードバックを適用し,ループの外側にむだ時間を配置した場合(先程のブロック線図の場合)の応答です.
両者が一致していることが結果からわかるかと思います.
また,Smith予測器なしでは不安定になっていたシステムが安定化できていることも確認できます.
閉ループシステムのナイキスト線図
最後に閉ループシステムのナイキスト線図を描いてみます.

凡例は先ほどの図のとおりです.
Smith予測器を適用した結果(赤の実線)と,閉ループシステムの外にむだ時間を出した結果(灰の破線)がぴったりと一致しています.
実用上の注意
Smith予測器はむだ時間を有するシステムに対して有効な手段ですが,以下の点に注意が必要です.
- コントローラ内部にノミナルモデル(プラント同定)が必要
- ノミナルモデルの同定精度によってはシステムが不安定になる
- 外乱に比較的弱い
最近(2018年)にはSmith予測器のアンチテーゼとして以下のような論文も出ています.
(ありがたいことにオープンアクセスです)
むだ時間の補償には他にも種々の方法が研究されてきましたが,今回紹介したSmith予測器は「制御性能の同定精度への依存度が高すぎるのではないか?」との主張のようです.
実際にノミナルモデルをプラントのパラメータから少し外してあげると,応答がかなり不安定寄りになってしまいます.
上記の論文では,Predictive PIというSmith予測器の特別な場合を利用しているようです.
同定精度の影響についてはMathWorksのページでも検討されているため,そちらを参照いただけると幸いです.
おわりに
現実で比較的遭遇しやすい,むだ時間を有するシステムにSmith予測器を適用する場合について考えてみました.
他の補償法としてPredictive PIを上げましたが,毎度喧伝しているモデル予測制御を利用することでもむだ時間をシステマティックに扱うことができます.
今回は出力側のむだ時間を取り上げましたが,入力側のむだ時間として長距離通信を介するシステムがあります.
先日の自動制御連合講演会(第61回)にてTubed-base model predictive controlを上記のシステムに適用した研究の発表がありました.
最新の入力が来ていない場合にはMPCの入力を2サンプル以上利用するという方法で,あまり他で見たことがなく面白かったです.
マルチレートのKalmanフィルタを構成する際,最新のセンサ値が得られなかった場合に予測分散を増加させるように組むことがあるのですが,似たようなアプローチなのかもしれないなあと.
残念ながらむだ時間の影響が強く出るシステムを取り扱ったことがないため,間違いや不足等あるかと思います.
その際はご指摘いただけるとありがたく思います.